Ratios and Proportions
Objective Learn the concepts of ratio and
proportion and to solve proportion problems.
Ratios
Mathematically, a ratio is simply a fraction viewed as a
division of two numbers. Its importance is that it is used to
compare two numbers (the numerator and the denominator of the
fraction). For example, the ratio of x to y is simply the
fraction 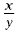 . A ratio can also be
written as x to y or x:y. . A ratio can also be
written as x to y or x:y.
In the following example you can see how a ratio compares two
numbers.
Example 1
In Ms. Cunningham's class there are 18 girls and 14 boys.
Write the ratio of boys to girls.
Solution
The ratio of boys to girls in the class can be written as 14
to 18 or 14:18 or 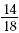 When simplified, this
ratio can also be expressed as 7 to 9 or 7:9 or When simplified, this
ratio can also be expressed as 7 to 9 or 7:9 or 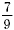
Proportions
An equation that states that two ratios are equal is called a proportion.
The equation 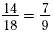 is a proportion. This
proportion can also be written as 14:18 = 7:9 is a proportion. This
proportion can also be written as 14:18 = 7:9
More generally a proportion will often involve variables.
Solving these problems usually involves elementary algebra,
because they involve solving for the value of a variable. To
solve these kinds of problems we use a process called cross
multiplying. The cross multiplying fact should be explained
carefully to your students.
Cross Multiplication Fact Suppose 0 y and 0 b
are not zero. Then 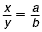 occurs exactly when xb
= ya. occurs exactly when xb
= ya.
Example 1
Solve 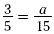 for a . for a .
Solution
Use the cross multiplication fact and solve the resulting
equation.
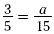
3(15) = 5( a )
45 = 5a
9 = a
Why is the cross multiplication fact true?
Notice that 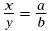 occurs exactly when occurs exactly when 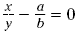 . Subtract these fractions by finding a
common denominator. . Subtract these fractions by finding a
common denominator.
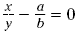 occurs exactly when occurs exactly when 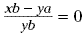 . .
Remember that a fraction equals 0 only when its numerator
equals 0. So for this equation, 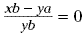 when xb - ya = 0 or when xb = ya. This is
the result of cross multiplying when xb - ya = 0 or when xb = ya. This is
the result of cross multiplying 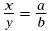 . .
The above discussion about why the cross multiplication fact
is true is a very important example of mathematical reasoning.
Namely, it uses a computational technique (subtraction of
fractions) to derive a general principle (cross multiplication
fact). In order to solidify this concept you should do many
examples of how this technique is applied.
|