Solving a Quadratic Inequality with Two Solutions
Once you have found the two solutions of the quadratic equation:
a · x2 + b
· x + c = 0,
you can write down the solution to the quadratic inequality. Table 1 below shows the solutions for each of the four basic types of quadratic inequality.
Note that in Table 1, the x-values that are solutions of the quadratic equation are
represented by the letters r1 and r2. We have assumed that r1 is the smaller of the two
solutions.
| Type of quadratic inequality |
Solution of quadratic inequality |
| a · x2 + b
· x + c > 0 |
x < r1 and x > r2 |
| a · x2 + b
· x + c < 0 |
r1 < x < r2 |
a · x2 + b
· x + c
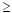 0
0 |
x
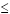 r1 and x r1 and x
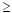 r2 r2
|
a · x2 + b
· x + c
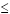 0
0 |
r1
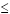 x x
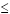 r2 r2
|
Table 1: Solutions for quadratic inequalities.
Figure 1 (below) shows why these inequalities match these particular solutions.
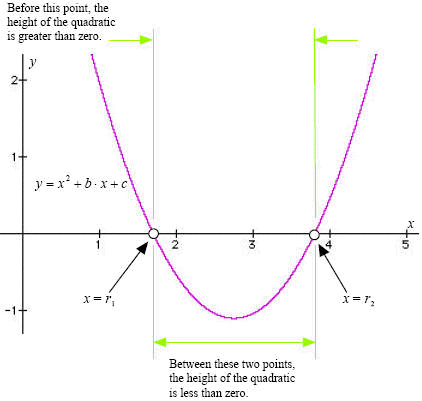
Figure 1.
Example
Solve the quadratic inequality:
4 · x2 - 2 × x + 3
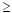 19. 19.
Solution
First, we must manipulate the given inequality to put it into one of the four basic forms.
To do this we can subtract 19 from both sides and then divide both sides by four. Note
that since we are dividing by a positive number, the direction of the inequality will stay
the same.
4 · x2 - 2
· x + 3
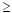 19. (Subtract 19 from both sides) 19. (Subtract 19 from both sides)
4 · x2 - 2
· x -16
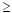 0 0
Now that the inequality is in one of the standard forms, we need to solve the quadratic
equation:
4 · x2 - 2
· x -16 = 0
Solving this quadratic equation with the quadratic formula gives:
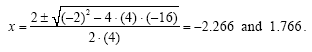
Consulting Table 1, the solution to the quadratic inequality consists of the two intervals
of x-values:
x
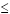 -2.266 and x -2.266 and x
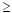 1.766. 1.766.
|