Common Logs
Notation for Common Logs
A logarithm has the form logbx, where x and b are real numbers,
x > 0, b > 0, and b ≠ 1.
A common logarithm has 10 for its base, b. Here are several examples of
common logs:
| log 10 1000 |
log 10 43 |
log 10 0.87 |
Common logs are often abbreviated by not writing the base.
For example, the common logarithms shown above can be written as:
Definition —
Common Logarithm
A common log is a log whose base is 10. It is written like this:
log x = log10 x Here, x > 0.
Common logs are useful since they have the same base as our number
system, which is base 10.
Finding Common Logs
We can find the value of some common logs by switching from
logarithmic notation to exponential notation.
Example 1
Find: log 10,000
Solution
| The base of a common log is 10. Therefore, write log 10,000 as log10 10,000.
Set x equal to log10 10,000.
Rewrite in exponential form.
Rewrite 10,000 as a power of 10.
Use the Principle of Exponential Equality
to solve for x.
So, log 10,000 = 4. |
x =
10x =
10x =
x = |
log10 10,000
log10 10,000
10,000
104
4 |
Note:
A factor tree can be used to write 10,000
as a power of 10.
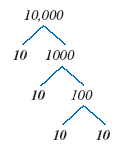
Thus,
10,000 = 10 · 10
· 10 · 10
= 104.
Principle of Exponential Equality:
If bx = by, then x = y. Here, b > 0 and b
≠ 1.
In many cases we cannot find the value of a common log by switching
from logarithmic notation to exponential notation.
For example, we can rewrite x = log 65 as 10x = 65, but it isn’t easy to
see what power of 10 equals 65.
We can approximate log 65 by noting the following:
1 = log10 10 is equivalent to 101 = 10
x = log10 65 is equivalent to 10x = 65
2 = log10 100 is equivalent to 102 = 100
So, log 65 must be between 1 and 2.
|