Writing a Rational Expression in Lowest Terms
A rational expression is a fraction where the numerator and the
denominator are polynomials. Reducing a rational expression to lowest
terms is similar to reducing an arithmetic fraction to lowest terms.
Procedure
To Reduce a Rational Expression to Lowest Terms
Step 1 Factor the numerator and denominator.
Step 2 Cancel pairs of factors that are common to the numerator
and denominator.
Example 1
Reduce to lowest terms:
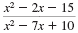
| Solution |
|
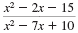| Step 1 Factor the numerator and denominator.
|
 |
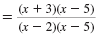| Step 2 Cancel common factors.
|
 |
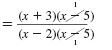| Simplify.
|
 |
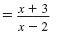Thus, the result is
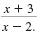
Note:
To factor x2 - 2x - 15:
• Find two integers whose product is -15 and whose sum is -2.
They are 3 and -5.
• Use these integers to write the
factorization (x + 3)(x - 5). To factor x2 - 7x + 10:
• Find two integers whose product is 10
and whose sum is -7.
They are -2 and -5.
• Use these integers to write the
factorization (x - 2)(x - 5).
Example 2
Reduce to lowest terms:
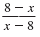
| Solution |
|
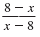| Step 1 Factor the numerator and denominator. |
| Factor -1 out of the numerator. Notice that in the numerator, -8 + x,
can be written as x - 8. |
 |
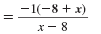
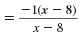| Step 2 Cancel common factors. |
| Cancel the common factor of x - 8.
Simplify. |
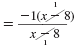 = -1 |
So, the fraction reduces to -1. Note:
Notice that in
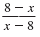, the numerator and
denominator are opposites.
Therefore,
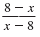reduces to -1.
Example 3
Reduce to lowest terms:
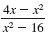
| Solution |
|
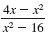| Step 1 Factor the numerator and denominator.
|
| Factor.
In the numerator, write 4 - x
as -1(x - 4). |
 |
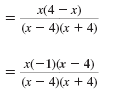| Step 2 Cancel common factors. |
| Cancel the common factor of x 4.
Simplify.
|
 |
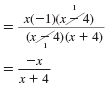Thus, the fraction reduces to
 .
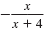Notice that 4 - x can be written as a
product where one factor is x - 4: 4 - x = -1(-4 + x) = -1(x - 4)
|
