Multiplying Fractions in General
Objective Learn how to multiply fractions.
Multiplying fractions is a little more difficult conceptually
than adding fractions, but the arithmetic procedure is much
easier. The discussion here will begin with the multiplication of
a fraction by a whole number, proceed to the multiplication of
two fractions each with numerator of 1, and then finish with the
multiplication of any pair of fractions.
What if we want to multiply two fractions that do not have 1
as their numerators? The following procedure can be used to
multiply any two fractions.
Key Idea
To multiply two fractions, multiply the numerators together to
find the numerator of the product, and multiply the denominators
together to find the denominator of the product. Simplify the
resulting fraction, if possible.
Example 1
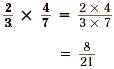
Why Does This Procedure Work?
We can draw a model. For example, to model the multiplication
of 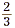 and and 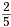 , we start with two line segments of the
same length. Divide one segment into 3 equal parts and darken 2
of the parts. Divide the other segment into 5 equal parts and
darken 2 of these parts. , we start with two line segments of the
same length. Divide one segment into 3 equal parts and darken 2
of the parts. Divide the other segment into 5 equal parts and
darken 2 of these parts.
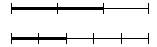
The two segments are then used as adjacent sides of a square
and the marks are used to divide the square into 15 regions of
equal size. The region formed by the two darkened parts of the
segments is then shaded.
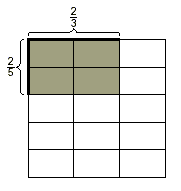
The shaded portion of the entire square includes 4 of the 15
small regions of equal size. Since each small region represents
the fraction 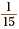 , the shaded portion
represents the fraction , the shaded portion
represents the fraction 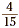 , which is the product of , which is the product of 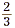 and and 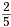 . .
|