Simplifying Expressions with Negative Exponents

Consider the expression

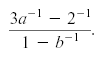
Using the definition of negative exponents, we can rewrite this expression as a complex fraction:

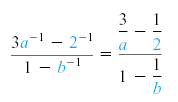
The LCD for the complex fraction is 2ab. Note that 2ab could also be obtained from the bases of the expressions with the negative exponents. To simplify the complex fraction, we could use Method B as we have been doing. However, it is not necessary to rewrite the original expression as a complex fraction. The next example shows how to use Method B with the original expression.

Example 1

A complex fraction with negative exponents

Simplify the complex fraction

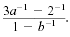
Solution

Multiply the numerator and denominator by 2ab, the LCD of the fractions. Remember that a^-1 · a = a⁰ = 1.

		Distributive property

Example 2

A complex fraction with negative exponents

Simplify the complex fraction

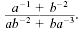
Solution If we rewrote a^-1, b^-2, b^-2, and a^-3, then the denominators would be a, b², b², and a³. So the LCD is a³b². If we multiply the numerator and denominator by a³b², the negative exponents will be eliminated:

		Distributive property

Note that the positive exponents of a³b² are just large enough to eliminate all of the negative exponents when we multiply.

The next example is not exactly a complex fraction, but we can use the same technique as in the previous example.

Example 3

More negative exponents

Eliminate negative exponents and simplify p + p^-1q^-2.

Solution

If we multiply the numerator and denominator by pq², we will eliminate the negative exponents:
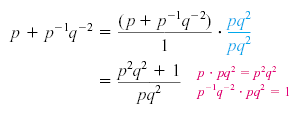