Graphing Inequalities in Two Variables
Objective Learn how to graph the solution
sets of inequalities in two variables.
It is important that you understand that solving an inequality
in two variables means describing the solution set for the
inequality, and that graphing it means specifying a whole region,
rather than a line or a curve. The solution procedure is similar
to that for linear equations, involving the Addition and
Multiplication Properties of Inequalities. That too should be
clear before starting to read this lesson, since it connects
these new ideas with ideas that are already familiar to you.
Linear Inequalities
A linear inequality is an expression similar
to a linear equation, except that it has an inequality symbol
rather than an equals sign.
| Linear
Inequalities |
Not Linear
Inequalities |
| 2x + 3y leq 7 + 5x |
x 2 + 5 geq y |
| x + 5 geq 2y - 5 |
xy > 7 |
| y < 5 |
y = x - 4 |
Solution Sets to Linear Inequalities
Let's begin with an inequality in two variables, say 3y + 5 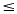 2x - 1. Then the solution set for the
inequality is the collection of all ordered pairs (x , y) for
which the inequality holds true. For example, the ordered pair
(7, 0) is in the solution set because substituting 7 for x and 0
for y makes the inequality true.
| 3(0) + 5 |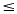
2(7) - 1 |
Replace (x, y) with (7, 0). |
| 5 |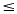
13  |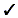
|
5 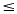13 is a valid inequality.
On the other hand, the ordered pair (2, 4) is not in the
solution set because substituting 2 and 4 for x and y ,
respectively, makes the inequality false.
| 3(4) + 5 |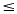
2(2) - 1 |
Replace (x, y) with (2, 4). |
17  |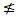
3 |
|
17 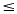3 is not a valid inequality.
|
