Polar Form of a Complex Number
Example 1
Writing a Complex Number in Polar Form
Write the complex number
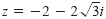 in polar form. in polar form.
Solution
The absolute value of z is
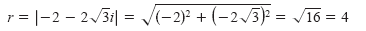
and the angle θ is given by
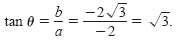
Because
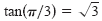 and because and because
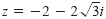 lies in Quadrant III, you
choose θ to be
θ = π + π/3 = 4π/3. Thus, the polar form is lies in Quadrant III, you
choose θ to be
θ = π + π/3 = 4π/3. Thus, the polar form is
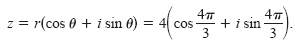
(See the figure below)
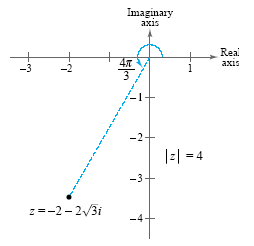
The polar form adapts nicely to multiplication and division of complex numbers.
Suppose you are given two complex numbers
z1 = r1(cos
θ1 + i sin θ1 )
and z2 = r2(cos
θ2 + i sin θ2 )
The product of z1 and z2 is
| z1
z2 |
= r1
r2 cos
θ1 + i sin θ1 )(cos
θ2 + i sin θ2 )
= r1
r2 [(cos
θ1cos θ2 - i sin
θ1sin θ2) + i(sin θ1cos θ2 +
cos θ1sin
θ2)] |
Using the sum and difference formulas for cosine and sine, you can rewrite this
equation as
z1 z2
= r1 r2
[(cos (θ1+
θ2) + i sin (θ1+ θ2)]
This establishes the first part of the following rule. Try to establish the second part on
your own.
Product and Quotient of Two Complex Numbers
Let z1 = r1(cos
θ1 + i sin θ1 )
and z2 = r2(cos
θ2 + i sin θ2 ) be complex
numbers.
| z1 z2
= r1 r2
[(cos (θ1+
θ2) + i sin (θ1+ θ2)] |
Product |
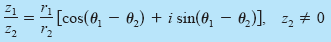 |
Quotient |
Note that this rule says that to multiply two complex numbers you multiply
moduli and add arguments, whereas to divide two complex numbers you divide
moduli and subtract arguments.
|