Linear Equations
Equations that can be written in the form ax + b = 0 where a
and b are real numbers, with a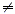 0,
are linear equations. Examples oflinear equations include 5y + 9
= 16 and 8x = 4
The following properties are used to solve linear equations.
PROPERTIES OF EQUALITY
For all real numbers a, b, and c:
1. If a = b then a + c = b + c Addition property of equality
(The same number may be addedto both sides of an equation.)
2. If a = b then ac = bc Multiplication property of equality
(Both sides of an equation may be multiplied by the same number.)
Solving Linear Equations
EXAMPLE
(a) If x -2 = 3 then x = 2 + 3 = 5 Addition property of
equality
(b) If x/2=3 then x = 2·3 = 6 Multiplication property of
equality
The following example shows how these properties are used to
solve lineare quations. Of course, the solutions should always be
checked by substitution inthe original equation.
EXAMPLE
Solve 2x - 5 + 8 = 3x + 2(2-3x)
Solution
2x - 5 + 8 = 3x + 4-6x Distributive property
2x + 3 = -3x + 4 Combine like terms
5x + 3 = 4 Add 3x to both sides
5x = 1 Add -3 to both sides
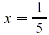 Multiply both sides by  .
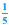Check by substituting in the original equation. The left side
becomes 2(1/5)-5+8 and the right side becomes 3(1/5)+2(2-3(1/5)).
Verify that both of these expressions simplify to 17/5.
|
