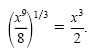Simplifying Expressions Involving Variables

When simplifying expressions involving rational exponents and variables, we must be careful to write equivalent expressions. For example, in the equation (x²)^1/2 = x it looks as if we are correctly applying the power of a power rule. However, this statement is false if x is negative because the 1/2 power on the left-hand side indicates the positive square root of x². For example, if x = -3, we get [(-3)²]^1/2 = 9^1/2 = 3, which is not equal to -3. To write a simpler equivalent expression for (x²)^1/2, we use absolute value as follows.

Square Root of x²

(x²)^1/2 = | x | for any real number x.

Note that the equation (x²)^1/2 = | x | is an identity. It is also necessary to use absolute value when writing identities for other even roots of expressions involving variables.

Example 1

Using absolute value symbols with exponents

Simplify each expression. Assume the variables represent any real numbers and use absolute value symbols as necessary.

a) (x⁸y⁴)^1/4

b)

Solution

a) Apply the power of a product rule to get the equation (x⁸y⁴)^1/4 = x²y. The lefthand side is nonnegative for any choices of x and y, but the right-hand side is negative when y is negative. So for any real values of x and y we have (x⁸y⁴)^1/4 = x²| y |.

b) Using the power of a quotient rule, we get

This equation is valid for every real number x, so no absolute value signs are used.

Helpful hint

We usually think of squaring and taking a square root as inverse functions, which they are as long as we stick to positive numbers.We can square 3 to get 9, and then find the square root of 9 to get 3— what we started with. We don’t get back to where we began if we start with -3.

Because there are no real even roots of negative numbers, the expressions a^1/2, x^-3/4, and y^1/6 are not real numbers if the variables have negative values. To simplify matters, we sometimes assume the variables represent only positive numbers when we are working with expressions involving variables with rational exponents. That way we do not have to be concerned with undefined expressions and absolute value.

Example 2

Expressions involving variables with rational exponents

Use the rules of exponents to simplify the following. Write your answers with positive exponents. Assume all variables represent positive real numbers.

Solution

b)	= a1/2 - 1/4	Use the quotient rule to subtract the exponents.
	= a1/4	Simplify.

c) (x1/2y -3)1/2	= (x1/2)1/2(y -3)1/2	Power of a product rule
	= x1/4y -3/2	Power of a power rule
		Definition of negative exponent

d) Because this expression is a negative power of a quotient, we can first find the reciprocal of the quotient, then apply the power of a power rule: