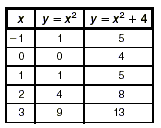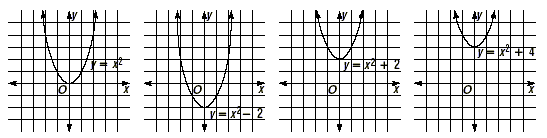
Parent and Family Graphs

Adding a Constant

Now consider a family of quadratic functions that are found by adding a constant to y = x ² . Graph the following functions on graphing calculators.

y = x ², y = x ² - 2, y = x ² + 2, y = x ² + 4

Try to find out what happens to the graphs of quadratic functions of the form y = x ² + c as c changes. Make sure your students notice the following.

1. The axis of symmetry for each parabola is the same, namely, the vertical line x = 0, which is the y -axis. This is because in y = x ² + c = 1x ² + 0x + c , a = 1, and b = 0. So, the axis of symmetry is the vertical line or 0.

2. The vertex of the parabola moves up or down, depending on the value of c in y = x ² + c . Since the axis of symmetry is the line x = 0 (or the y -axis), the x -coordinate of the vertex is 0. To find the y -coordinate, substitute x = 0 into the equation.

y = x ² + c

y = 0 ² + c Replace x with 0.

y = c

So the y -coordinate of the vertex is c . In other words, the vertex of the parabola given by the function y = x ² + c is the point at (0, c ). So if we add c to y = x ² , the vertex moves up by c . If we subtract c from y = x ² , the vertex moves down by c .

3. The parabolas all have the same size. They have just been shifted up or down by c units because the y values of the function y = x ² + c are exactly c units more than the y values of the function y = x ² . This is called a vertical translation. You can see this pattern with a table like the one shown below.

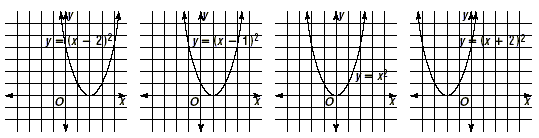
Adding a Constant Before Squaring

Now consider the family of quadratic functions of the form y = ( x + d ) ² , where d is some constant. Graph the following examples on graphing calculators.

y = ( x - 2) ² , y = ( x - 1) ² , y = x ² , y = ( x + 2) ²

Try to figure out what happens to the graphs of quadratic functions of the form y = (x + d) ² as d changes. Make sure you understand the following.

1. The axis of symmetry shifts to the left or right, depending on whether d is positive or negative. To understand this algebraically, expand the expression y = ( x + d ) ² = x ² + 2dx + d ² . In this expression, a = 1, b = 2d , and c = d ². So the axis of symmetry has the equation . For example, if d is positive, the line x = - d is the vertical line shifted to the left d units from the y -axis.

2. The vertex of the parabola moves left or right, depending on the value of d in y = ( x + d ) ² . Since the axis of symmetry is the line x = - d , the x-coordinate of the vertex is - d . To find the y -coordinate, substitute x = -d into the equation.

y = ( x + d ) ²

= ( - d + d ) ² Replace x with - d .

= 0 ² or 0

So the y-coordinate of the vertex is 0. In other words, the vertex of the parabola given by the function y = ( x + d ) ² is the point at ( - d , 0).

3. The parabolas all have the same size. They have just been shifted to the right or left by d units. This is called a horizontal translation .